Questo è un post pasquale dove cerco di fare un modello della caccia alle uova come se fosse la produzione di una risorsa minerale. Viene fuori che un modello semplice basato sulla dinamica dei sistemi può essere equivalente a quello di Hubbert per l'estrazione del petrolio. Possiamo avere il "Picco delle Uova" e viene anche fuori che il picco può avere la forma asimmetrica del "Picco di Seneca." Così, anche questo modello semplice conferma quello che il filosofo romano ci aveva detto tanto tempo fa: che la rovina è molto più rapida della fortuna. (Immagine da uptownupdate)
Per quelli di voi che non conoscono la tradizione del coniglio pasquale, posso dire che negli Stati Uniti i conigli fanno le uova e non solo. Per Pasqua fanno uova colorate. La tradizione è che il coniglio pasquale sparpaglia queste uova nel giardino e poi i bambini si divertono a cercarle. E' un gioco che piace molto ai bambini e può durare anche a lungo se il coniglio è stato abbastanza cattivo da nascondere le uova molto bene e se il giardino è grande.
Una curiosità della caccia alle uova è che somiglia alla ricerca dei minerali. Con i minerali, proprio come con le uova, bisogna cercare dei tesori nascosti e, dopo che uno ha trovato i minerali "facili" (o le uova), trovare quelli ben nascosti può richiedere un bel po' di lavoro. Così tanto che di solito ci sono delle uova che rimangono nascoste, proprio come ci sono dei minerali che non saranno mai estratti.
Ora, se la ricerca dei minerali è simile alla ricerca delle uova pasquali, forse potremmo imparare qualcosa di molto generale se proviamo a fare un piccolo esercizio di modellizzazione. Possiamo usare la dinamica dei sistemi per costruire un modello che risulta essere capace di descrivere sia la caccia alle uova pasquali, sia il comportamento in stile "Hubbert" della produzione dei minerali. Il modello ci può anche dire qualcosa di come la dinamica dei sistemi può essere usata per fare dei modelli "a misura di mente" (per usare un'espressione coniata da Seymour Papert). Allora, proviamo.
Nella dinamica dei sistemi, i modelli si basano sul concetto di "stock," ovvero la quantità delle cose che il modello descrive (in questo caso, le uova). Gli stock non rimangono costanti (altrimenti il modello sarebbe ben poco interessante) ma cambiano col tempo. Diciamo che uno stock "fluisce" in un altro. In questo caso, le uova cominciano nello stock che chiamiamo "uova nascoste" e si trasferiscono nello stock che chiamiamo "uova trovate". Poi, dobbiamo anche considerare un altro stock, il numero dei bambini.
Per fare il modello, dobbiamo fare delle assunzioni. Potremmo dire che il numero di uova trovato per ogni intervallo di tempo è proporzionale al numero dei bambini, che potremmo prendere come costante. Poi, potremmo anche dire che diventa sempre più difficile trovare uova via via che ce ne sono di meno di nascoste. Questo è tutto quello di cui abbiamo bisogno per fare una versione molto di base del modello.
Queste sono tutte considerazioni che potremmo scrivere in forma di equazioni, ma qui possiamo usare un metodo ben noto nella dinamica dei sistemi che costruisce le equazioni partendo da una versione grafica del modello. Tradizionalmente, gli stock sono mostrati come rettangoli ("scatole") e i flussi come frecce a due tratti. Frecce a singolo tratto collegano fra loro le varie scatole e flussi. per questo modello, ho usato un programma chiamato "Vensim," fatto da Ventana systems (freeware per uso personale o accademico). Allora, ecco qui la versione più semplice possibile del modello della caccia alle uova pasquali.
Come vedete, ci sono tre scatole, ognuna col nome della cosa che contiene. La freccia a due tratti mostra come lo stesso tipo di stock (uova) fluisce da una scatola all'altra. L'aggeggio a forma di farfalla è la "valvola" che regola il flusso. La produzione dipende da tre parametri: 1) l'abilità dei bambini nel trovare le uova, 2) il numero dei bambini (qui preso come una costante) e 3) il numero di uova nascoste che rimangono.
Il modello produce un output che dipende dai valori dei parametri. Più in basso, vediamo i risultati per la produzione con 50 uova iniziali, 10 bambini e un'abilità uguale a 0.006. Notate che il numero di uova varia in modo continuo. Ci sono altri metodi per fare modelli che utilizzano numeri interi, ma è così che funziona la dinamica dei sistemi. Come tutti i metodi di modellizzazione, è un'approssimazione della realtà
Qui, la produzione va quasi a zero via via che i bambini esauriscono la loro riserva di uova. In questa versione del modello abbiamo dei bambini-robot che continuano a cercare all'infinito e, alla fine, troveranno tutte le uova. Nella pratica, dei bambini reali si stancheranno e a un certo punto smetteranno di cercare. Ma questo modello può essere una descrizione approssimata di una vera caccia alle uova quando c'è un numero costante di bambini, cosa che si verifica in pratica quando ce ne sono pochi.
Possiamo fare un modello più generale? Immaginiamo che ci siano molti bambini e che non tutti si stanchino allo stesso momento. Assumiamo allora che si stanchino in modo casuale. Poi, possiamo assumere che la caccia alle uova diventa così interessante che attira un numero crescente di bambini? Questo si può simulare. Un modo semplice di farlo è di assumere che il numero di bambini che arrivano è proporzionale al numero di uova prodotte. Ecco allora un modello basato su queste ipotesi (notate le nuvolette. Indicano che non teniamo conto della dimensione degli stock dove i bambini vanno, oppure da dove arrivano)
Questo modello è un tantino più complicato, ma non tanto. Notate che ci sono due nuove costanti, "k1" e "k2," utilizzate per regolare la variazione dello stock dei bambini. Qui ne troviamo anche una terza (k3) che utilizzeremo più tardi in un modello leggermente diverso. I risultati per la produzione di uova sono i seguenti:
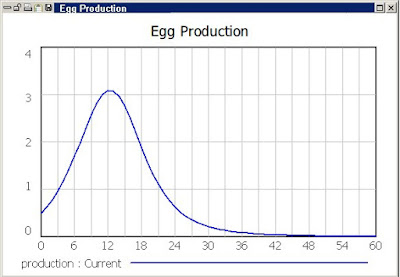
Ora la produzione di uova mostra un bel picco, dalla forma a campana. Questa forma è una caratteristica "robusta" del modello. Ci si può divertire a cambiare i valori delle costanti, ma questo è quello che si ottiene, normalmente: un picco simmetrico. Come probabilmente giù sapete, questa forma è la caratteristica del modello di Hubbert della produzione petrolifera, dove il picco si chiama di solito "Picco di Hubbert." In effetti, questo semplice modello di caccia alle uova pasquali è equivalente a un modello che ho usato, insieme al mio collaboratore Alessandro Lavacchi, per descrivere casi storici di produzione di risorse non rinnovabili. (si veda questo articolo pubblicato su "Energies" e qui per un riassunto)
Possiamo giocherellare un altro po' con il modello. Che ne dite di immaginare che i bambini possono imparare a cercare meglio le uova, via via che il tempo passa? Questo si può simulare assumendo che il parametro "abilità" aumenti di una tacca per ogni uovo trovato. I risultati? Beh, ecco un esempio:
Abbiamo ancora un picco, ma adesso è diventato asimmetrico. Non è più il picco di Hubbert ma quello che ho chiamato il "picco di Seneca" secondo quello che ha scritto il filosofo romano Seneca quando ha notato che la rovina è di solito più rapida della fortuna. In questo esempio, la rovina arriva così rapidamente proprio perché si cerca disperatamente di evitarla. E' un classico esempio di "spingere le leve nella direzione sbagliata", come ci ha raccontato Donella Meadows qualche tempo fa. Non è per niente intuitivo ma, quando si sfruttano risorse non rinnovabili, aumentare l'efficienza non è una buona idea.
Ci sono molti modi di spellare un coniglio, per così dire. Così, questo modello può essere modificato in molti modi, ma possiamo fermarci qui. Credo che ci abbia dato una buona illustrazione di come giocherellare con dei modelli "a misura di mente" e come questi modelli basati sulla dinamica dei sistemi ci possono dare qualche interessante idea di come funziona il mondo reale. Detto questo, buona Pasqua a tutti!
(In Italia non si usa molto la ricerca delle uova pasquali, ma se qualcuno avesse voglia di prendere dei dati per questa Pasqua, potremmo provare a confrontarli con il modello!)